SUMMARY

Adding a per-head parameterized scaling factor to the query-key attention scores (analogous to adding a learnable temperature to the softmax) slightly improves performance transformer performance.

[Update 11/2024: If this interests you some recent work re-examines the role of softmax in a similar vein. DeepMind’s softmax is not enough proposes adapting softmax temperature based on the entropy of the input, applied to the language modeling head only. I had no luck with entropy-based adaptation, see “what didn’t work” section at bottom.]

INTRODUCTION

About a year ago I wondered if the softmax used in attention would benefit from a learnable temperature term. A single parameterized scalar value could help the model essentially flatten or sharpen the distribution of attention scores. Since different heads take on different roles, the model might benefit from the option of using temperature per-head terms to further differentiate the different heads.

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{temp * QK^T}{\sqrt{d_k}}\right)V$

where $temp$ is a single parameterized scalar value.

Each attention head at each layer has its own temperature term, so in total the model adds (heads * layers) new parameters. In practice the temperature term can equivalently be factored out and used to multiply just the queries or just the keys prior to self-attention computation. This allows one to still use hard-coded library implementations like flash attention.

Note that the normal sqrt(head_dimension) scaling factor remains to control for variance.

NB: Also note that temperature here multiplies the scores pre-softmax rather than dividing them as is customarily done. If it helps you can regard the term here as inverse temperature. In this work, low temperature results in flat, high entropy distributions and high temperature results in spiky, low entropy distributions.

HYPOTHESIS AND RESULT

If the model’s parameterized temperature terms a) change significantly from their initial value of 1.0 and b) show high variance in values across heads at a given layer, then we can take this as loose evidence these temperature terms are being utilized by the model effectively.

I played around with this idea and found that these two conditions a) and b) hold. Furthermore, a model with these temperature terms provides a slight decrease in loss against baseline for pretty much every language modeling architecture and setup I’ve used. (NB: all such architectures and setups are small: <1B parameters, <.25B tokens.) This is at the minimal cost of (heads * layers) additional parameters.

Adding per-head temperature term (yellow line) results in a slightly improved language modeling loss over baseline (black line) wandb

Each line shows the mean value of the temperature term per layer +/- variance across temperature terms per layer.

Another view, another model post-training

Examining the query values across a single layer, you can see distinct splits where each head starts and ends. This effect is exaggerated with parameterized temperature terms.

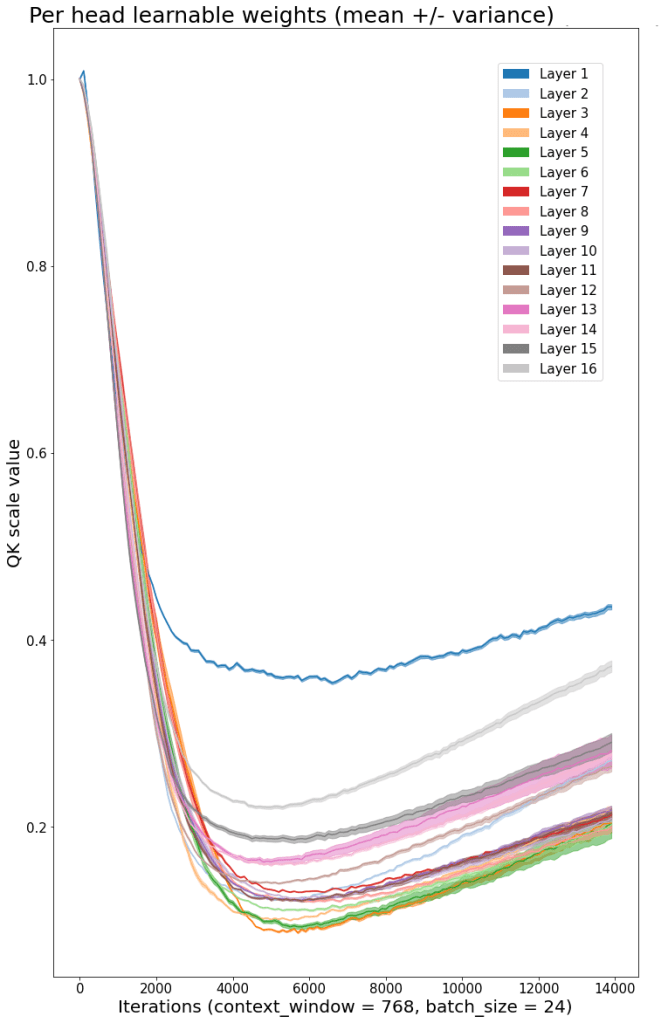
Additionally, inspecting the value of the temperature terms provides another perspective on model behavior. For example, the temperature values of a model that turns out to be too deep given its width / insufficiently wide given its depth looks like this:

A .5B param model with 32 layers trained for 4000 iterations. Temperature terms initialized at .5

If you retrain this model configuration but with 18 layers instead of 32, the model now has the same or better loss and the temperature values look like this:

Suggesting that the later layers were redundant. This diagnosis could clearly be derived other ways, for example by examining the gradient or skip connections. Nevertheless it serves as a very simple diagnostic tool helping me to design and examine the behavior of models.

FUTURE WORK

In future work, one could pair the temperature values per head against an analysis of the head function. This could help shed light on why different layers learn very different temperature values for different heads.

For example, different assumed head roles (copy suppression, induction, negation, name mover) may benefit from sharper or smoother distributions depending on how specific or “all or nothing” their function is. A head focusing on induction might benefit from very sharp scores that can categorically identify whether or not a sequence has occurred in the past context, whereas a head with a more nuanced task may benefit from much smoother attention scores.

All this to say, the per-head temperature values may be beneficial because they provide an easy mechanism for the model to dial up or down the entropy of attention scores in a given head.

RELATED WORK

I’ve neglected to write up these results for a while. This is partly because the idea is very simple, and partly because I’ve since seen very close variations of this idea in a few places.

YaRN, for example, includes this trick, though the value of $t$ is fixed. I asked one of the authors where this came from, but he didn’t have a source and said they included it because it worked.

The self-attention mechanism for YaRN includes a (non-parameterized) temperature scaling value for the pre-softmax query-key scores.

This led me to believe that this idea of temperature scaling the attention scores was diffuse enough that it was in the category of “trick” that many already knew, so writing it up wouldn’t add anything.

By pure coincidence I was recently led to the closest source of this idea I can find thanks to BirchLabs, who led me to an existing implementation in the k-diffusion library and the probable source, “Query-Key Normalization for Transformers“

Query-key normalization does two things: a) L2 normalization for queries and keys along the head dimension, b) per-head learnable scalar value for attention scores, eliminating the traditional sqrt(head_dimension) scaling factor.

Query-key normalization self-attention equation

(Amusingly, I have not only seen but have actually implemented this paper before (in building Memorizing Transformers we normalize the key values to mitigate model drift interfering with the KNN key value lookup) but I clearly skimmed and only focused on the normalization part of this paper.)

The authors include some interesting analysis of the the temperature terms, hypothesizing that lower entropy distributions of the attention scores improve learning by enabling “winner takes all” computation:

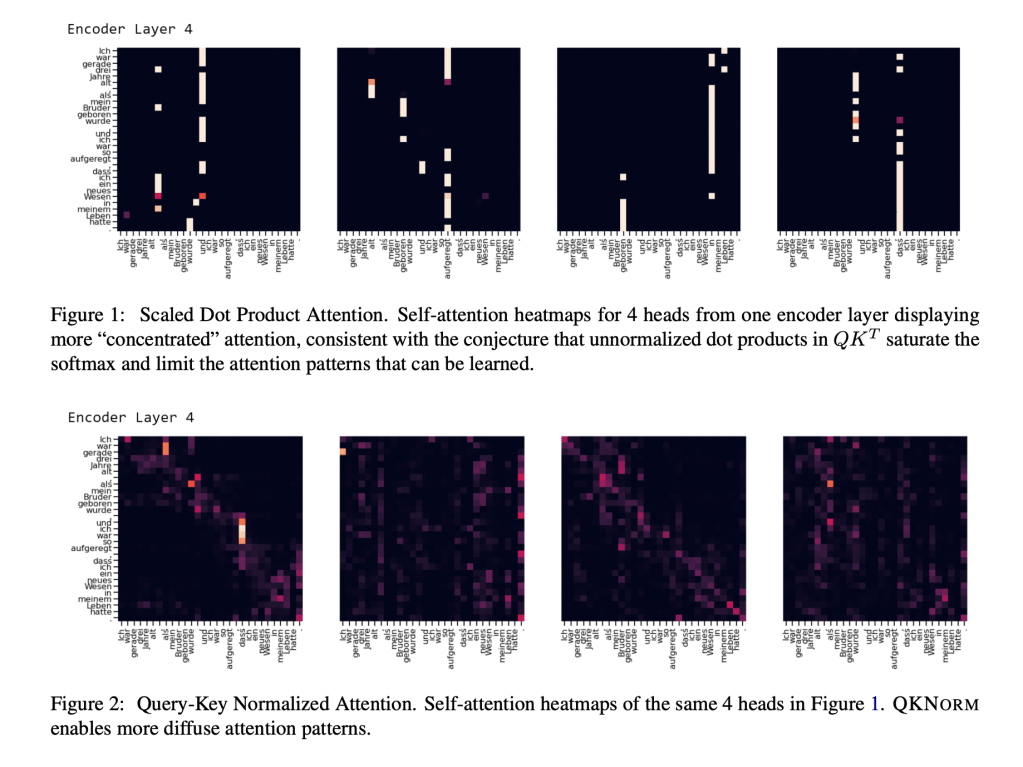
So if you googled the right keywords, I hope you have ended up here and my hunting around will be of some use to you.

WHAT DIDN’T WORK

There are a lot of things you could try here. Nothing worked noticeably better than the simple initial idea of per layer, per head, single scalar value that multiplies the attention scores.

Scaling post-softmax
Scaling by (1,d) temperature values instead of (1,1) per layer per head.
Scaling per layer and not per head (heads share one value per layer)
Scaling per head and not per layer (layers share one value per head)
Wrapping the scaling value in tanh or sigmoid (in order to change the shape of the gradient) seems roughly equivalent
Attempts to use entropy, HHI, variance per example, etc. anything where we try to rescale the attention scores based on some statistic about the current data sequence being passed through didn’t work markedly better than simple per-layer-per-head scalers. Scaling the scaling term, adding a bias, etc. did not work.
- Example: “sigmoid-entropy-scaling-corrected-bias-.3-scales”, meaning per head per example entropy is calculated from the post-softmax query@key values and then scaled with a sigmoid function with scales initialized at .3 and bias initialized at 0. We then rerun the query@key and softmax using these values to scale the query@key pre-softmax attention scores, s.t. high or low entropy sequences can receive an appropriate “correction” to be made sharper/smoother.
  - Temperature = (scale1 * sigmoid(scale2 * (sequence_entropy – bias1)))
  - The idea is scale1 can adjust the magnitude, scale2 adjusts the sharpness of the sigmoid, and bias lets us recenter the function over a reasonable value given the data.
    - Some work went into trying to help the bias value. Consider that a 512 length sequence is split into 512 examples of 1,2,3,…510,511 token lengths. The entropy of the first 1-length example is always -log(1.0 * 1).0 = 0, and the last 511-length sequence has max possible entropy of -log(1/511)=~6.2, which is close to what’s observed empirically. Initializing the bias as 0, or scaled linearly from 0-6.2 across increasing length examples, or logarithmicaly from 0-6.2…none of it made much of a difference.
    - However this is way too convoluted and involves creating the attention scores, then calculating the entropy per example, then using that value to rescale the values, then computing the new attention scores….too much work for too little gain.