SUMMARY

We propose a lightweight and simple mechanism, “weak recurrence,” to incorporate information from previous time steps. This method simply adds a gated weighted sum over the previous n tokens between the attention and feedforward components of a transformer layer. This modification results in improved performance.

[Code, Log/notes]

INTRODUCTION

In recent years there is renewed interest in recurrent models for language modeling. While transformers have been the dominant architecture across domains for several years, architectures like Mamba (the latest in a series of state space / recurrent models) have introduced new ideas that result in improved modeling performance and, crucially, better computational efficiency.

Others have explored the incorporation of recurrent computation blocks into standard transformer architectures. How best to incorporate this recurrence into transformer architectures remains unknown. There are a number of outstanding questions related to architecture search along this line:

Where in the architecture is recurrence applied? In the attention block, feedforward block, in between? Replacing one of these blocks?
Which previous states are used? One previous state, multiple, or all?
How are the previous state(s) aggregated? Convolution, addition, concatenation, linear map, custom kernel, etc. How to effectively concentrate or represent the previous state?
By what operation is the previous state combined with the current input? Gating, addition, Hadamard? Is this operation input-dependent?

In search of a simple, lightweight, and effective way to incorporate recurrence into a transformer model, we explore various permutations and present the best-performing result, called weak recurrence.

Weak Recurrence

We allow each example in a batch to access the representation of previous examples directly following self-attention computation, just prior to the feed-forward computation. While self-attention allows each token to attend to every other token equally following the query, key, and value projections, this method allows each example to directly access the result of this self-attention for the few immediately preceding examples which are in theory highly relevant. In other words, each token not only attends to all other tokens, it also attends to how the previous n examples attended to all other tokens.

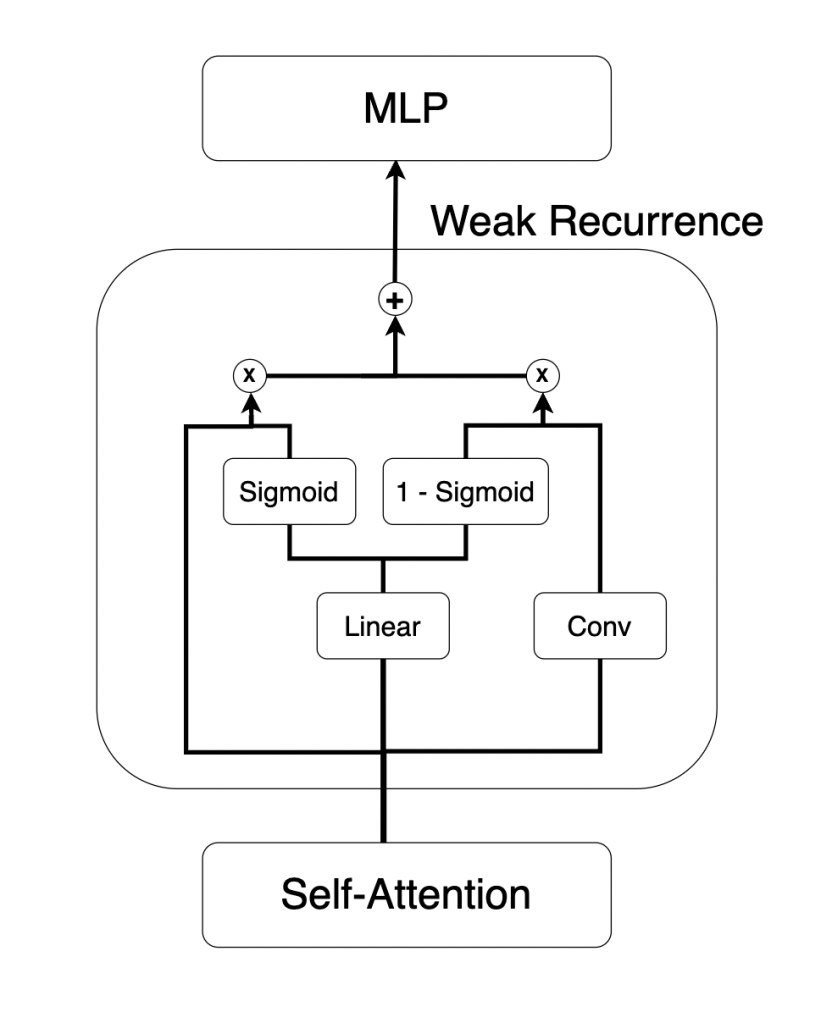
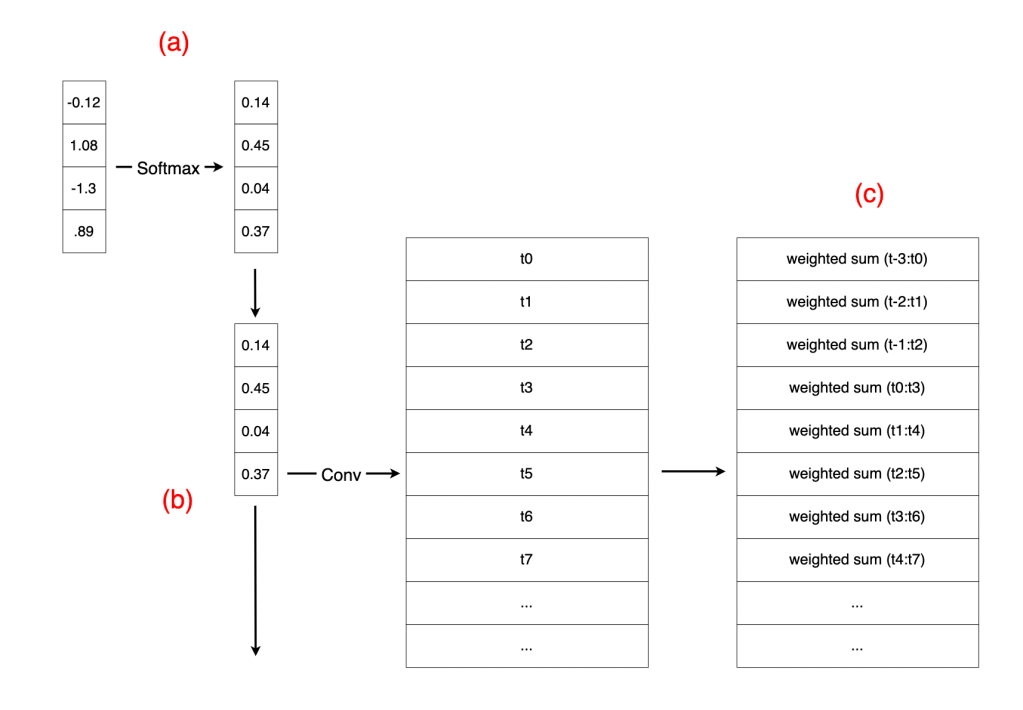
In weak recurrence, our input is the output of the attention layer, $x$ , which passes through two main branches. One branch has a linear transformation $W_g$ followed by a sigmoid gate $g$ . The other branch passes a convolution over the $n$ previous examples in the batch with a set of weights $W_{conv}$ that has been passed through softmax such that the convolution is simply a weighted combination over the past $n$ examples that sums to 1. The gate $g$ from the first branch is used to weight the original input, while $1-g$ is used to weight the convolution over past examples. These two terms are then added together.

$g = sigmoid(W_g (x))$

$prev= conv(x; n, softmax(W_{conv}))$

$g * x + (1-g) * prev$

Demonstration of convolution over past examples. The convolution weights are first passed through a softmax (a), which is then applied to the previous n states (b) to obtain a weighted sum over past examples (c).

Here is a pytorch implementation:

MAIN RESULT

Loss per iteration: weak recurrence (yellow) (350M parameters) outperforms a standard model (black) (334M parameters) wandb

Loss per GFLOP: weak recurrence (yellow) (350M parameters) outperforms a standard model (black) (334M parameters) wandb

Loss per iteration: weak recurrence with temperature and weighted skip connections (purple) (350M parameters) outperforms a standard model (black) (334M parameters) wandb

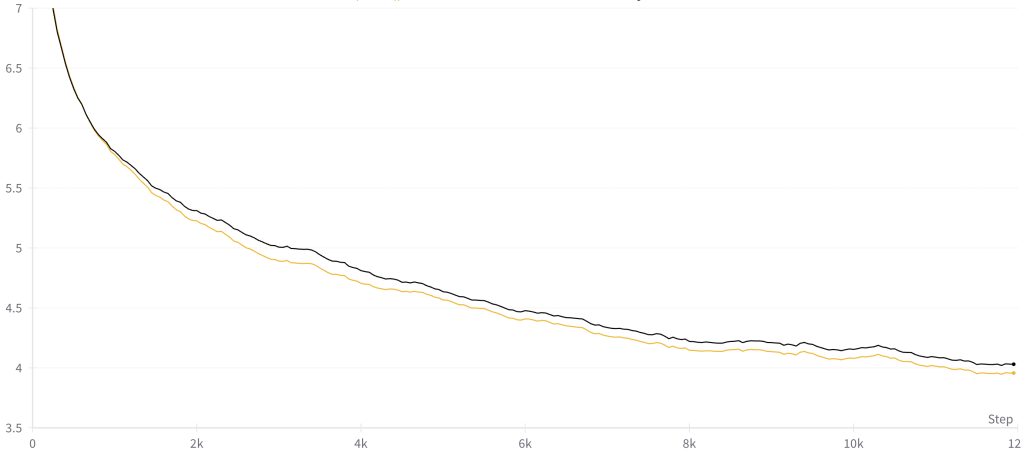
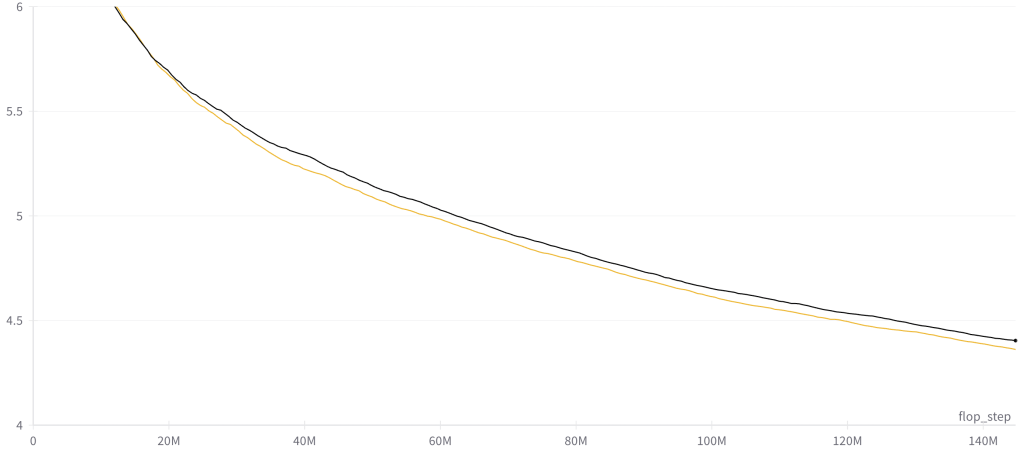
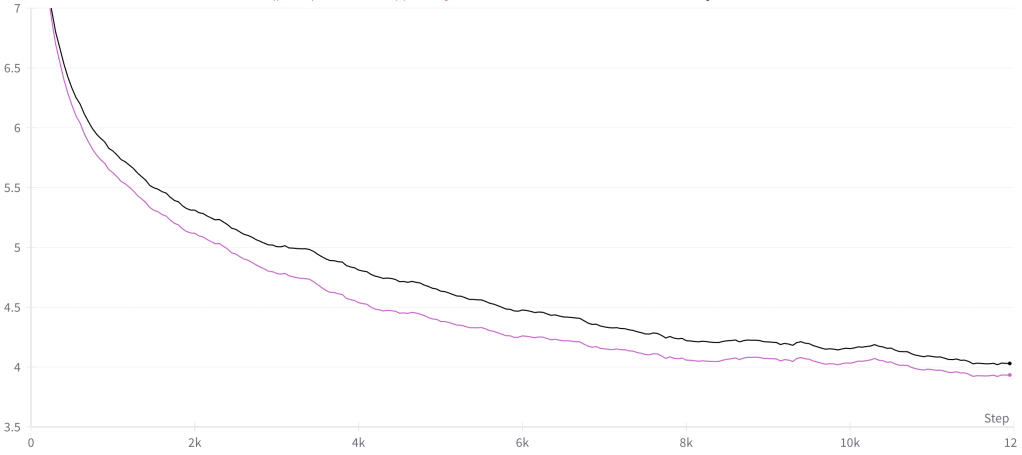
DISCUSSION

The original idea was to simply incorporate, for each token, the attention outputs from the immediately preceding tokens since these tokens tend to be extremely relevant. The key goal was to have a cheap, recurrence-like computation (hence “weak” recurrence) that let us view previous tokens – rather than the outputs of previous computation – as previous time steps. From there it is about the set of design questions asked at the beginning of this post, essentially where and how to incorporate this information into the existing transformer architecture with minimal complexity and overhead.

Per-layer attention score heatmaps in GPT-2-small, (built using TransformerLens). Note, especially in the early layers, how higher scores tend to reside on or near the diagonal, indicating high attention scores for immediately preceding tokens.

Specifically, while a token might attend heavily to the token immediately preceding it, it might also be useful to see how that token in turn computed its attention scores over all previous tokens.

This was first attempted over the previous token(s) by applying a downshift matrix, which was then generalized into convolution. Both the sigmoid gating over a linear transformation of the input (input-dependent gating, inspired by Mamba‘s “selection mechanism”) and the softmax applied over convolution weights prior to convolution were both key details (as was initializing the convolution weights equally as 1 / n).

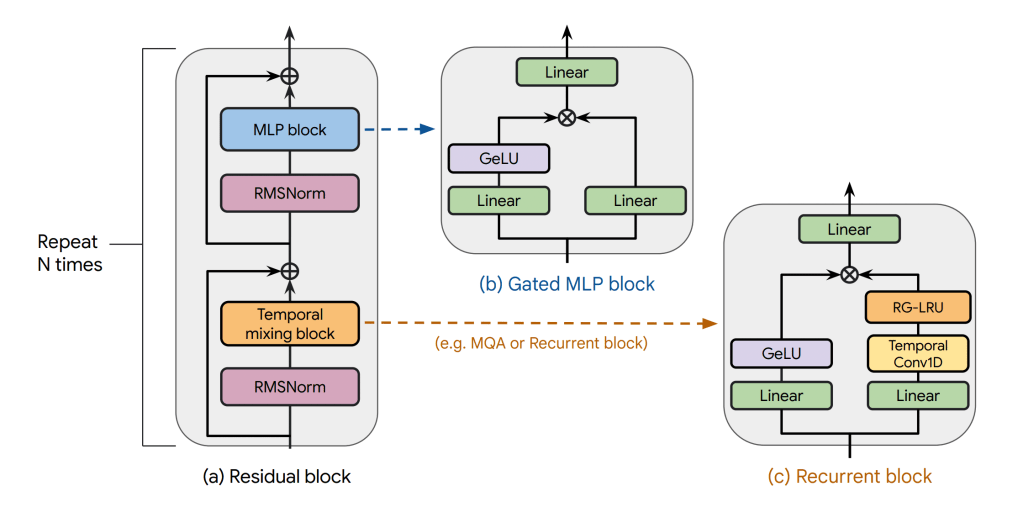
Post-training (softmaxed) convolution weights of the previous n states at each layer. All weights are initialized equally as 1 / (number of previous steps). For early layers the immediately preceding tokens learn higher weights during training. For later layers the previous tokens learn approximately equal weight.

Griffin

Weak recurrence can be seen as a close relative of Griffin‘s RG-LRU block (seen in RecurrentGemma), and the overall model architecture shares the similarity of placing the recurrent block between attention and MLP. Variation 7.1 (see experimental log below) closely mimics the Griffin gating mechanism to our setup, which performed nearly as well as weak recurrence, though the implementation and comparison is not exact due to inherent differences in the previous example tensors. Griffin alternates RG-LRU with attention every other layer, though I have not tried this approach or done any ablation experiments to see if weak recurrence could be removed from some layers (I suspect it could be removed from later layers without much detriment).

State space models

Although the definition of “previous state” / “previous time step” is very different from that used in state space model literature (H3, Mamba, S4, LSSL, etc.) there is strong overlap in the methods and mechanisms of incorporating previous states with current computation. This is only a brief mention of the current RNN and state space literature, which I can’t do justice to beyond some familiarity with the work out of Hazy Research.

Evolution of the model

Over the course of these experiments there was a great amount of re-inventing components from modern state space literature as well as re-applying mechanisms from older LSTM literature.

Of particular importance, this project is a long list of negative results that I would like to share.

WHAT DIDN’T WORK

It’s important to document what did not work.

Inside the feedforward block: methods of incorporating previous tokens

There are many different ways of incorporating data from previous states with data from the current state.

Notes and accompanying code. (Very messy, please reach out if you would like to discuss.)

Here are some methods that did not work as well as the version of weak recurrence presented above:

Single scalar sigmoid gate over previous tokens
Concatenation of current token and previous token with linear transformation back to appropriate shape
- Sigmoid gating applied to this output
Sigmoid following a linear transformation over the current token, serving as a gate over current and previous tokens (Mamba style input-dependence)
GRU style gating
Griffin-style RG-LRU (with and without added norm for stability)
Weak recurrence with no softmax applied over the convolution weights
Weak recurrence with a linear transformation directly after convolution
Weak recurrence with linear transformation directly prior to convolution
Weak recurrence with concatenated current and previous token before data-dependent linear transformation
Weak recurrence with wider convolution kernels (various widths)
Input-dependent linear transformation that then transforms the previous token (based on “The Illusion of State in State-Space Models”, see also this thread from the author)
And more…

Inside the attention block: attention_score @ attention_score

Incorporating the information about raw attention scores for each token. In other words, token n attends to all other tokens, and then we augment it directly with the attention scores such that tokens have access to how all the other tokens attended to them.

Notes with some code examples. (Very messy, please reach out if you would like to discuss.)

The primary mechanism is to matrix multiply the masked attention score with itself and view this as a matrix where each token can see how all past tokens attended to it. There are multiple ways of incorporating this information:

Norming
Adding
Sigmoid gated addition
Concatenation and linear transformation
Masked linear transformations over the attention scores
Applying the values matrices and adding the results
Variations pre-softmax, post-softmax

All in all, none of these variations made much of a difference. A very reasonable theory is that self-attention already works incredibly well, and modifications will have negative or no effect.